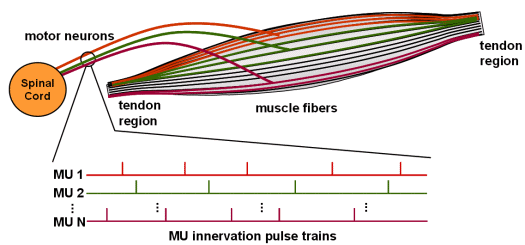
Fig.1: Schematic picture of human muscle with different Motor Units (MU).
System Software Laboratory has rich and long-lasting experiences in processing of biomedical signals. The first activities in this field were initiated when the laboratory was established in 1989. At that time, the main focus was on the analysis of electrocardiograms (ECG). In collaboration with the Gorenje company from Velenje, Faculty of Electrical Engineering from Ljubljana, and Institute Jožef Stefan from Ljubljana, a special device called CardioA was developed for acquisition, monitoring and analysis of multi-lead ECG signals recorded during an exercise test. The device was clinically validated at the Hospital of Topolšica and in the Rehabilitation Centre at Krapinske Toplice, Croatia.
Later on, the analysis of needle and surface electromyograms (EMG) was addressed through fruitful contacts and project collaboration with other prominent bioengineering laboratories, especially with the Institut für Signal- und Informationsverarbeitung at the ETH in Zurich, Switzerland, Laboratoire d’Automatique de Nantes, France (today called Institute de Recherche en Communications et Cybernetique de Nantes), and LISiN at Politecnico di Torino, Italy. Current research activities deal mainly with the decomposition of surface EMG signals detected by high-density arrays of surface electrodes.
These pages describe briefly some of our recently developed surface EMG decomposition techniques, which are exemplified with their typical decomposition results. More consistent description of the presented methods can be found in corresponding papers (see the reference list at the end of this page). For clarity reasons, the problems of surface EMG generation, detection, and decomposition are also briefly outlined.
Advanced medical diagnosing resides with precise information which can be obtained from the measured physiological data. When it comes to the neurophysiology, quantitative measures of neuromuscular degeneration and effectiveness of treatment are of paramount importance. Moreover, in order to support evidence-based medicine, a deeper understanding of the muscle alternations (neuropathies, pain, muscle weakness, etc.) and their relations to work conditions, immobilization and overtraining is required. Speaking about quantitative indicators of neuromuscular system condition, there is no real alternative to electromyogram (EMG) signals, i.e. the electrical signals traversing the neuromuscular system.
Human muscles comprise thousands of tiny fibres which, when electrically excited, contract and, at the same time, produce a measurable electrical potential, called action potential (AP). APs emerge at the neuromuscular junction about the middle of the muscle body, and propagate along the fibres to both directions towards the muscle tendons. The neural system, responsible for the activation of muscle fibres, conducts electrical pulses from the brain to the muscles. During voluntary muscle contractions the whole sequences of electrical pulses, so called innervation pulse trains (IPT) are transferred by the same motoneuron (Fig. 1). Fibres which are innervated by the same nerve contract synchronously (Fig. 2) and form a basic functional muscle unit, the motor unit (MU).

Fig.1: Schematic picture of human muscle with different Motor Units (MU).
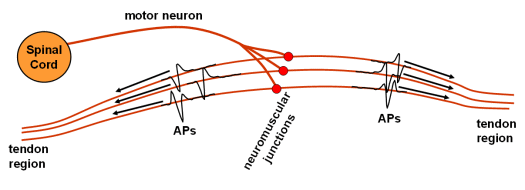
Fig. 2: Schematic picture of individual motor unit with travelling Action Potentials (APs).
One of the most important, but also most challenging issues, still lacking the adequate robustness and reliability, is decomposition of EMG signals into their constituent components, i.e. to the motor unit action potentials (MUAPs) and to the innervation pulse trains (IPTs). Namely, measuring the electrical potential at an arbitrary position in space, the MUAPs from different MUs appear superimposed in both time and space, forming very complex patterns (Fig. 3). Moreover, the passive electric media surrounding the muscle fibres acts as a low-pass filter which decreases the MUAP amplitude and increases its duration.
On the other hand, reconstructed MUAPs and IPTs represent one of the most important quantitative measures of neuromuscular degeneration and effectiveness of motor rehabilitation. They are used in advanced research and clinical investigations concerning various neuromuscular pathologies, work-related disorders, and myoelectrical manifestations of fatigue, etc. Generation, acquisition and decomposition of multichannel surface EMG signals is schematically depicted in Fig. 4.

Fig. 3: Contributions from individual MUs (left), and their temporal summation (superimposition) as detected by the pick-up electrode (right).
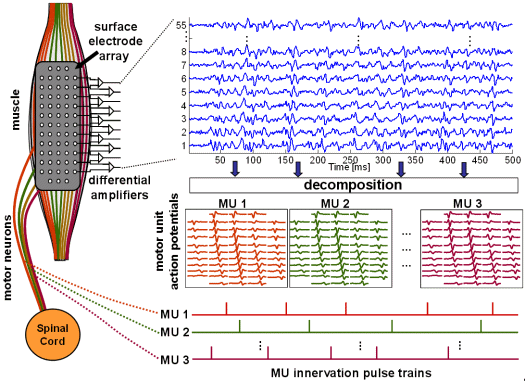
Fig. 4: Schema of SEMG signals generation (left), acquisition (top) and decomposition (bottom right).
The existing computer-aided EMG decomposition methods are mainly focused on the invasive intra-muscular EMG signals (Fig. 5). Decomposition techniques based on pattern recognition and clustering in the time domain, on spatial filtering, and on time-frequency and time-scale analysis, report controversial results and fail when a large number of components (MUAPs) become superimposed. Most recent pattern recognition techniques make use of graph theory and artificial intelligence to successfully cope with the complex superimposed MUAPs patterns. Unfortunately, their use is restricted to the invasive and painful needle EMG, to be performed by properly trained medical personnel in a hospital environment.
Surface electrodes offer numerous advantages when compared to the invasive needle ones:
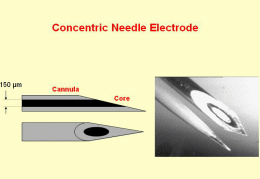

Fig. 5: left: invasive needle electrodes (from www.casaengineering.com/instr.htm; right: arrays of non-invasive surface electrodes (from www.lisin.polito.it).
The recent development of flexible high-density adhesive 2D arrays of surface electrodes opened the possibilities of recording up to a few tens or even hundreds of SEMG signals simultaneously. At the same time, with the increase of computer performance, more sophisticated and computationally complex separation techniques, capable of processing and combining the information from such large multichannel recordings, became feasible. However, although many attempts were made in the past no approach developed so far enables a complete and reliable reconstruction of IPTs out of the SEMG signals. The main reasons can be identified as follows:
SEMG recordings can be modelled as a multi-channel linear, time-invariant system, as long as they have been taken in stable, controllable, and stationary measurement session. This implies an isometric muscle contraction and avoiding of the appearance of fatigue-induced changes. Dealing with sampled multi-channel EMG recordings, the discrete, shift-invariant MIMO modelling is most feasible. Each source (channel input) in such MIMO system is considered a MU innervation pulse train triggering the muscle, while the system responses (channels) correspond to the MUAPs as captured by a spatial filter (pick-up electrodes). The individual EMG measurements represent the model outputs.
The shapes of system responses in the assumed MIMO system are of no importance. Hence, any property of MU (e.g. its depth in the muscle tissue, the number of fibres and their conduction velocities, etc.), as well as the properties of the detection system (the spatial filter used, inter-electrode distance, etc.) influencing the shapes of MUAPs can be modelled in the system responses.
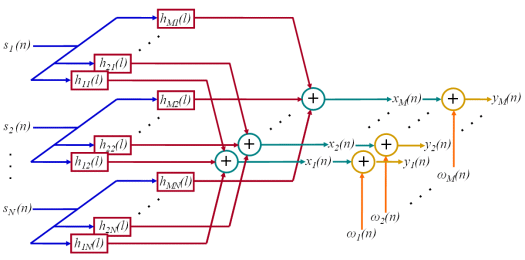
Fig. 6: Assumed convolutive MIMO system with sources (IPTs), system responses (MUAPs), measurements, noise, and noisy measurements. The operation of convolution is depicted by rectangles, addition with circles.
The innervation pulse trains are typically modelled as a time sequences of delta pulses. This is a very coarse approximation because the pulses in neurons are actually action potentials and hence at least a few ms long. Moreover, they occupy more than two different values (when sampled with high-enough frequency) and can hardly be modelled as a true delta pulses. Nevertheless, only the MUs’ responses (MUAPs) to innervation pulse trains are measured by the surface electrodes, while the shape of neuron potentials do not impact the shapes of MUAPs. Therefore, action potentials in a motor neuron can be conceptually replaced by true delta pulses. It should be stressed here that this “conceptual replacement” is nothing else but a very useful convention.
Time-frequency (TF) analysis is one of the most frequently used tools in the filed of signal processing. It also plays an important role in blind source separation, because it enables us to separate sources with Gaussian distribution. Although it is most frequently used for separation of multiplicative mixtures, it is becoming more and more important also when it comes to the separation of convolutive mixtures.
Very efficient approach to separation of multiplicative mixtures of independent nonstationary sources was introduced by A. Belouchrani and M. Amin [1]. Their method exploits the differences in energy locations of sources in time-frequency domain and is based on the joint diagonalization of spatial time-frequency distribution (STFD) matrices which are constructed from the time-frequency distributions of all possible pairs of measurements. Similar approach was also suggested for general convolutive mixtures of non-stationary signals [1, 2]. In [2], for example, convolutive mixtures were converted to multiplicative ones by simply adding delayed repetitions of measurements. Such a conversion also changes the number of sources which now form block diagonal STFD matrices. Hence, with joint block diagonalization [3] of observation spatial time-frequency distribution matrices several versions of each source can be retrieved, but only up to an unknown filtering effect [2].
Our time-frequency based SEMG decomposition approach is based on the work of A. Belouchrani and M. Amin, however, it additionally suggests the construction of diagonal source STFD matrices. These latter matrices are processed into a joint-diagonalization scheme (instead of joint block diagonalization), which provides an estimation of the system responses (MUAPs detected on different electrodes) and sources up to the scale factor and the phase shift. More details about the TF-based SEMG decomposition method can be found in [4].
The theory of higher-order statistics (HOS) has been well established, also in the field of MIMO systems. It has been shown that the system’s responses can be deconvolved whenever the system’s input can be modelled as an independent identically distributed (i.i.d.), zero-mean, random white signals. Although suffering from a very high computational complexity, HOS-based methods have many nice properties. They can be successfully applied when the number of sources highly exceeds the number of measurements, while the superimpositions of impulse responses do not hinder a thorough decomposition. Moreover, by being insensitive to all Gaussian random processes the cumulants of order higher than two are also inherently resistant to the Gaussian noise.
As already discusses ITPs are usually modelled as a sparse positive pulse sequences and cannot be strictly treated as i.i.d. white random signals. However, this does not corrupt the higher-order cumulants, as long as they are computed at the lags that do not exceed the minimum inter-pulse distance. In the case of biomedical signals, the minimum inter-pulse distance in ITPs exceeds the length of MUAPs. Therefore, when properly used, the theory of HOS can be applied to the SEMG signals.
HOS-based SEMG decomposition approach developed in SSL is implemented in two-steps. Firstly, a multivariate version of w-slice method is applied in order to extract coarse approximations of MUAPs. Secondly, these coarse estimates are refined by non-linear Newton-Gauss iteration.
Among various approaches having been proposed for MIMO system identification, we want to rely upon those with as little a priori information needed as possible. One of them is so called multivariate w-slice method [7]. Beside the minimum number of system channels to be modelled, the only additional information needed in this approach is about the values of the starting samples of system-channel responses.
Multivariate w-slice method is based on Barlett-Brillinger-Rosenblatt equation [6]. Firstly, a set of nonlinear equations is formed by comparing the model-based and the observation-based cumulant estimates. Afterwards, taking the casualty of multichannel SEMG signals into consideration, the system of non-linear equations is solved by applying the inverse of special weight matrix W to the causal part of properly formed cumulant matrix. The matrix W can be constructed out of anti-causal part of abovementioned cumulant matrix, as described in [8].
The first approximations of the system-channel responses can further be improved by iterative non-linear Newton-Gauss optimization. In each step of iteration the cost function is formed by fitting the model-based cumulant estimates to the observation-based cumulant estimates. Afterwards, the values of MUAP estimates are updated by Newton-Gauss formula and the model based cumulant estimates recalculated. This optimization procedure is repeated until the convergence is reached [8].
Convolution Kernel Compensation (CKC) method is a novel decomposition technique developed entirely in SSL. It exhibits a very low computational complexity and is suitable for real-time signal decomposition of both convolutive and multiplicative mixtures of pulse sources. In contrast with other decomposition techniques, the CKC method works well also when the number of active MUs is slightly underestimated, if the MU firing patterns partly overlap and if the measurements are noisy
Realizing it is much easier to estimate pulse sources than general mixing coefficients (MUAPs) the CKC method is based on a completely novel decomposition concept. Throughout its derivation we ignored all the information about the mixing process and focused strictly on the properties of pulse sources. In other words, we tried to cancel the interfering effect of the mixing process (MUAPs) and reconstruct the sources (IPTs) directly. This has at least two significant advantages. Firstly, estimation of mixing process is prone to both estimation errors and noise, and provides good quality results only if the given mixing process is well-conditioned. Secondly, estimation of mixing process is time consuming approach. Direct compensation of the mixing process will, hence, speed up the decomposition. Detailed description of CKC method can be found in [5].
All SEMG decomposition techniques developed in SSL were tested on both synthetic and real SEMG signals. In the sequel, the simulation and experimental protocols are briefly described, along with some typical results of aforementioned decomposition techniques.
The synthetic signals were generated by the advanced SEMG simulator built by the LISiN laboratory at Politecnico di Torino, Italy. The number of active MUs was set to 5, 10 and 20, respectively, while SNR ranged from 0 dB to 20 dB, in steps of 5 dB. In each simulation run the depth of MUs (uniformly distributed over [3,10] mm), their firing rate (normally distr. with mean and st. dev. of 15±4Hz), the number of fibres (uniformly distr. over [50,300]), and conduction velocity (normally distr., 4 ± 1m/s) were randomly selected. The detection system with 1×1 mm electrodes arranged in 10 lines and 5 columns was centred over innervation zone (columns aligned with the direction of fibres). Single differential recordings were sampled at 1024 Hz. The simulated signals are illustrated in Fig. 7. The results obtained by different decomposition techniques are exemplified in Figs. 8 – 13.
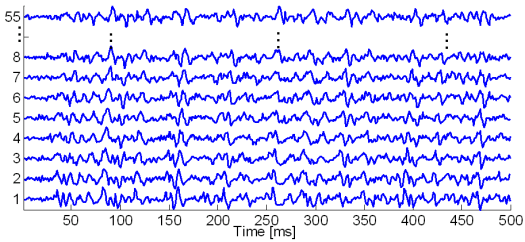
Fig. 7: Generated synthetic signals with 20 active MUs. For clarity reasons, only a portion of generated SEMG signals is depicted.
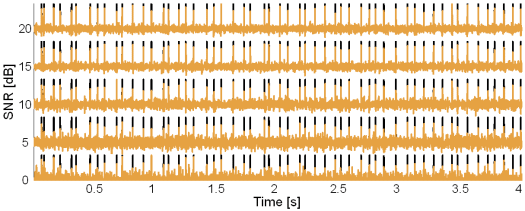
Fig. 8: Original synthetic innervation pulse trains (black) and the pulse trains reconstructed by the method based on TF distributions (brown) in the case of 5 active MUs and at SNR = 20, 15, 10, 5 and 0 dB.
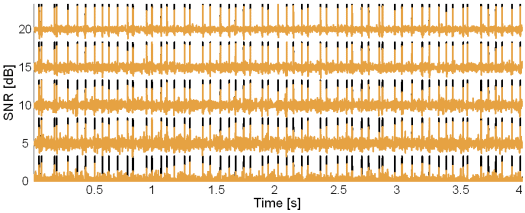
Fig. 9: Original synthetic innervation pulse trains (black) and the pulse trains reconstructed by the method based on TF distributions (brown) in the case of 10 active MUs and at SNR = 20, 15, 10, 5 and 0 dB.
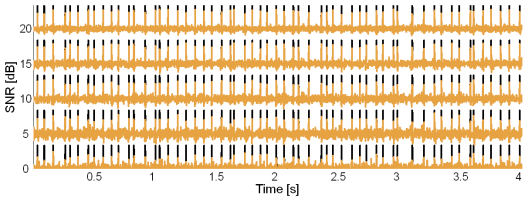
Fig. 10: Original synthetic innervation pulse trains (black) and the pulse trains reconstructed by the CKC method (brown) in the case of 10 active MUs and at SNR = 20, 15, 10, 5 and 0 dB.
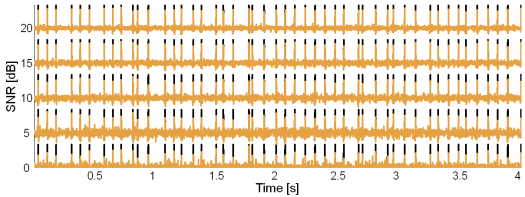
Fig. 11: Original synthetic innervation pulse trains (black) and the pulse trains reconstructed by the CKC method (brown) in the case of 20 active MUs and at SNR = 20, 15, 10, 5 and 0 dB.
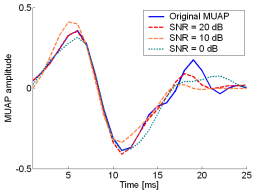
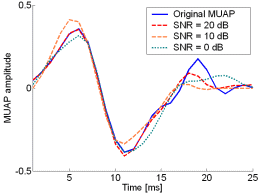
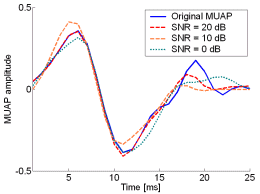
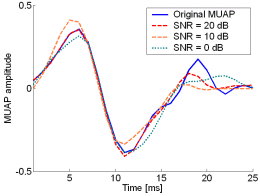
Fig. 12: The MUAPs, reconstructed by w-slices from the synthetic surface EMG signals of length 30720 samples in the case of 5 active MUs and at SNR=20 dB (red), SNR=10 dB (orange), SNR=0 dB (green). Reference values are depicted with blue solid lines.
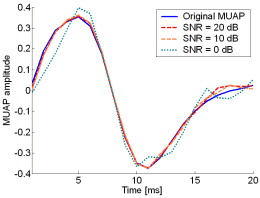
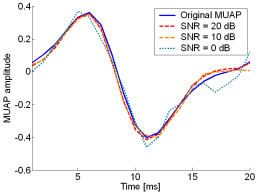
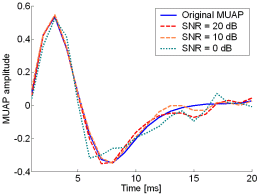
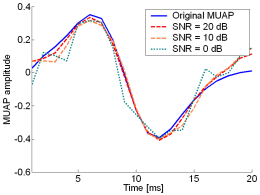
Fig. 13: The MUAPs, reconstructed by CKC method from the synthetic surface EMG signals of length 30720 samples in the case of 10 active MUs (upper plots) and 20 active MUs (lower plots) at SNR=20 dB (red), SNR=10 dB (orange), SNR=0 dB (green). Reference values are depicted with blue solid lines.
61 electrodes (5 columns and 13 lines, columns aligned with muscle fibres) from the dominant biceps brachii muscle of 9 healthy male subjects (age 26.8 ± 2.2 years, height 179 ± 7 cm and weight of 72.1 ± 8.3 kg). The aforementioned electrode array was developed by the LISiN laboratory at Politecnico di Torino, Italy. Isometric mucle contractions were performed at 5% and 10% of the maximum voluntary contraction (MVC) force, respectively. Single differential recordings were amplified, band-pass filtered (3 dB bandwidth, 10 Hz-500 Hz) and sampled at 2500 Hz. The acquired signals are exemplified in Fig. 14. The results obtained by the CKC method are exemplified in Figs. from 15 to 19. Figs 20 and 21 depict the results of other two decomposition techniques in comparison with the results of CKC method.
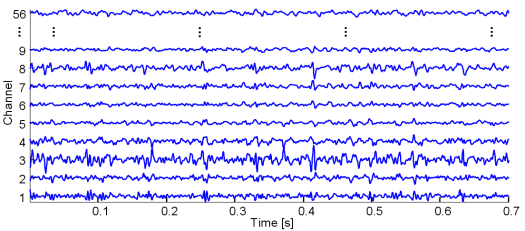
Fig. 14: Real SEMG signals recorded with a matrix of 61 electrodes from the dominant biceps brachii muscle of young healthy male subject. Isometric contraction was performed at 10% of the maximum voluntary contraction. For clarity reasons, only a portion of generated signals is depicted.
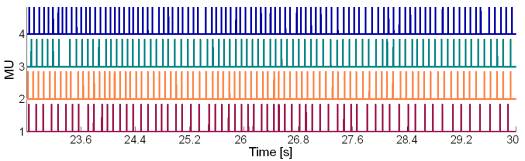
Fig. 15: The MU innervation trains reconstructed by the CKC method from 30 s long real SEMG signal. SEMG was recorded during an isometric 5 % MVC measurement of the dominant biceps brachii of healthy male subject (age 26 years, height 176 cm, weight 68 kg). Only a part of the reconstructed innervation trains is depicted.
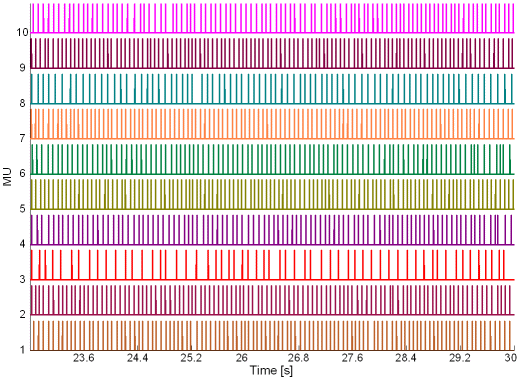
Fig. 16: The MU innervation trains reconstructed by the CKC method from 30 s long real SEMG signal. SEMG was recorded during an isometric 10 % MVC measurement of the dominant biceps brachii of healthy male subject (age 31 years, height 180 cm, weight 65 kg). Only a part of the reconstructed innervation trains is depicted.
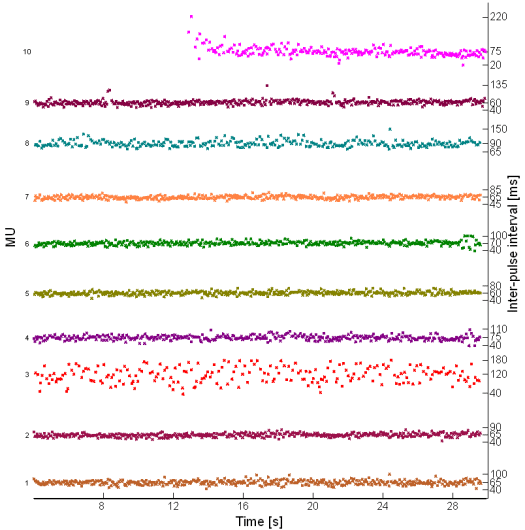
Fig. 17: Inter-pulse interval in innervation pulse trains reconstructed by the IC method from 30 s long real SEMG signal. SEMG was recorded during an isometric 10 % MVC measurement of the dominant biceps brachii of healthy male subject (age 25 years, height 170 cm, weight 63 kg).
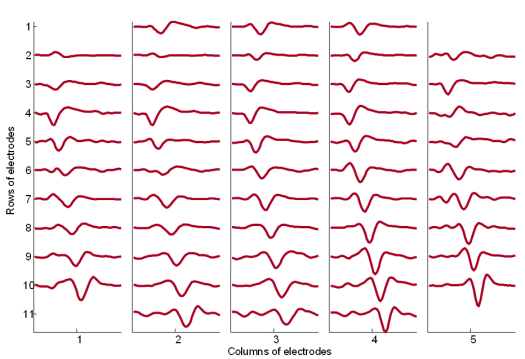
Fig. 18: The MUAPs corresponding to MU 2 (Fig. 14) reconstructed by the spike triggered sliding window averaging technique (210 averages) from 30 s long SEMG signals. The MUAPs are depicted with respect to the relative position of the corresponding pick-up electrodes. Surface EMG signals were recorded during an isometric 5 % MVC measurement of the dominant biceps brachii of healthy male subject (age 26 years, height 176 cm, weight 68 kg).
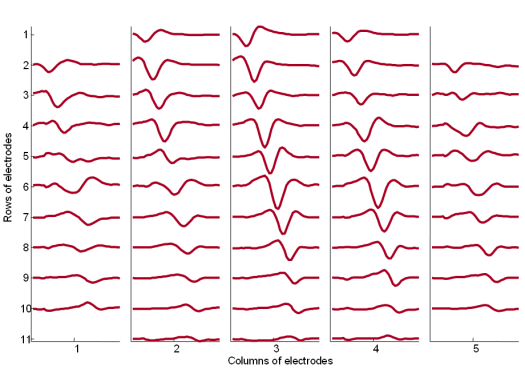
Fig. 19: The MUAPs corresponding to MU 1 reconstructed by the spike triggered sliding window averaging technique (293 averages) from 30 s long SEMG signals. The MUAPs are depicted with respect to the relative position of the corresponding spatial filter. Surface EMG signals were recorded during an isometric 10 % MVC measurement of the dominant biceps brachii of healthy male subject (age 31 years, height 180 cm, weight 65 kg).

Fig. 20: Innervation pulse trains reconstructed by the method based on TF distributions (brown) and their comparison to the results of the CKC method (black): a) subject 1, ME 3 b) subject 6, MU 1, c) subject 6, MU 3, d) subject 6, MU 5, e) subject 8, MU 2, f) subject 8, MU 3, g) subject 9, MU 2 in h) subject 9, MU 4. The SEMG signals were recorded during the isometric 10 % MVC measurements of the dominant biceps brachii of nine healthy male subjects (age 26.8 ± 2.2 years, height 179 ± 7 cm, weight 72.1 ± 8.3 kg). The pulses reconstructed by the IC method are normalised to 1.
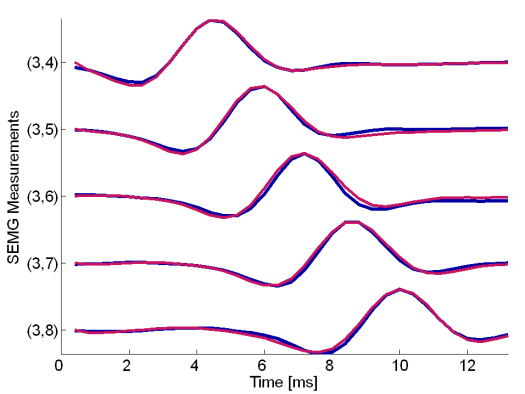
Fig. 21: MUAPs of the third MU reconstructed by HOS-based method (red) and by the IC method (blue). Surface EMG signals were recorded during the isometric 5 % MVC measurements of the dominant biceps brachii muscle of subject 6 (age 28 years, height 182 cm, weight 70 kg).
This work was supported by: