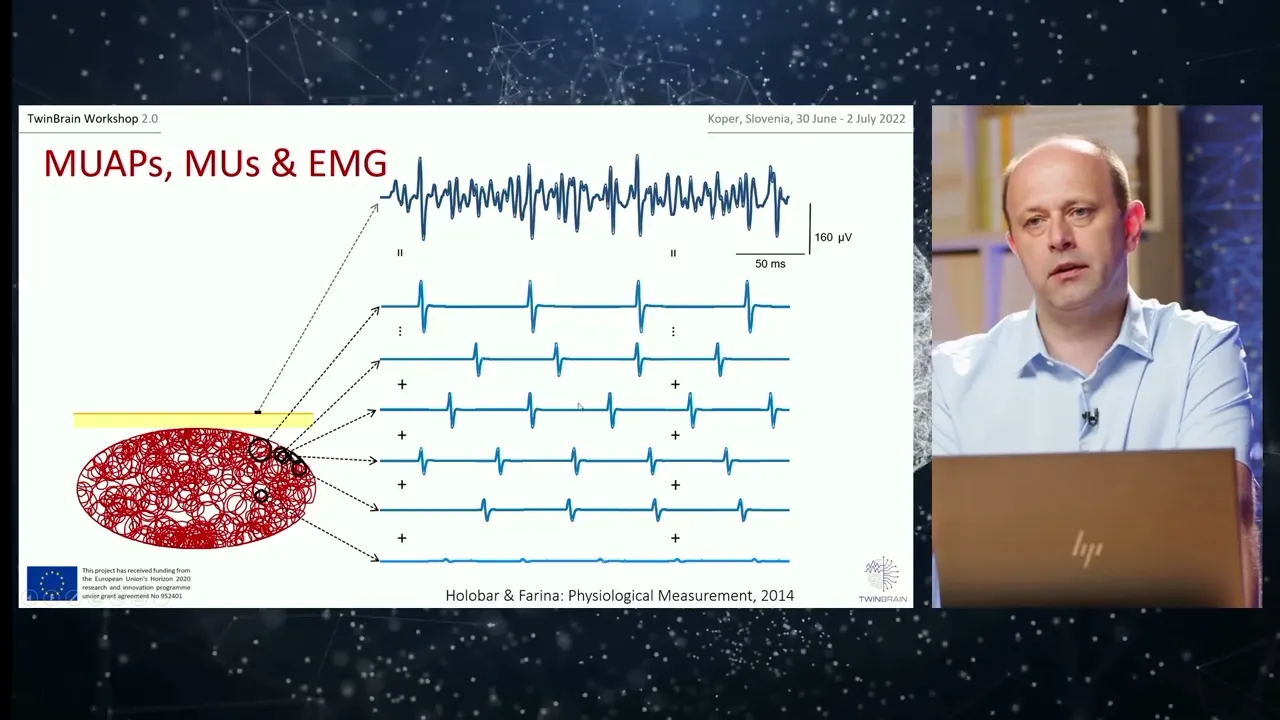
Author: Andrej Šoštarič
Mentor: Asoc. Prof. Dr. Damjan Zazula
Co mentor: Asst. Prof. Dr. Nikola Guid
Date: Oct. 1995
Decomposition and Reconstruction of One-Dimensional Signals Using Orthogonal Transforms and Multirate Sampling
Keywords: digital signal processing, decomposition, reconstruction, frequency spectrum, multirate sampling, orthogonal transform, short-time Fourier transform, discrete Karhunen-Loéve transform, orthonormal base, wavelet transform, scaling function, mother wavelet, multiresolution representation, phyramid algorithm, quadrature-mirror filter, EMG signal.
UDK: 621.391 : 681.32
Abstract: In this work, short-time Fourier transform, discrete Karhunen-Loéve
transform and wavelet transform are being used for analysis of nonstacionary
digital signals. Time-dependent frequency content and multiresolution
approximations of discrete signals are being studied in more detail. Basic
principles of multirate sampling are presented and their reflection on the
frequency spectrum, caused by increasing or reducing the sampling frequency
rate, is being observed. Multiresolution representation is introduced by means
of discrete and continuous wavelet transform. The assumption that discrete and
continuous wavelet transforms are very appropriate for analysis of nonstacionary
signals was confirmed with extended tests and comparison of the results
obtained. While discrete wavelet transform is being used for analysis of details
and approximations of signals at different resolutions (it could also be used
for signal compression), continuous wavelet transform is suitable for 2D
representations and analysis of power distributions in the scale-frequency
plane.