Author: Dean Korosec
Mentor: Asoc. Prof. Dr. Damjan Zazula
Co mentor: Asst. Prof. Dr. Nikola Guid
Date: Apr. 18, 1996

Modeling and Decomposition of Compund Signals

Keywords: digital signal processing, modeling, decomposition, parametric searching, electromyograph signals, simulation of electromiyograms, linear modeling, AR, MA and ARMA models, second order statisctics, autocorrelation, random noise.

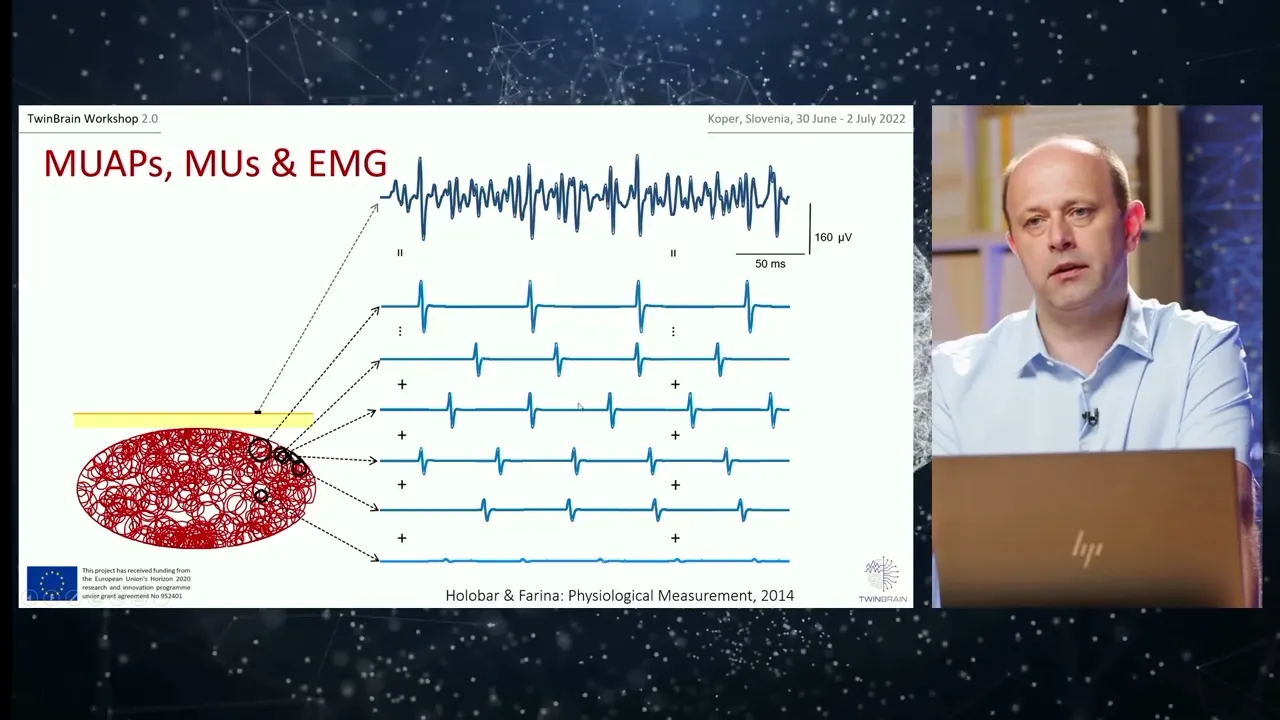
Abstract: We discuss some of the approaches to signal modeling. Because we also deal with parametric modeling of the known unimodal and multimodal methods are collected after the introduction. This is the theoretical groundwork on which our later described decomposition method is based. But before that we describe the origin and nature of the electromyographic signals, both needle and surface. This physiological model is then directly used in the specifications for the software simulator of such signals, given in the first half of the third chapter. In the rest of the same chapter our iterative parametric method of decomposition is presented. Method adopts action potentials generated by modified line-source model as basic shapes. Evaluation on synthetic and real signals shows that the method is relatively insensible for additive noise and specially suitable for the modeling of surface electromyograms.

Another way of describing surface electromyograms is to use linear models. AR model of relatively low orders (2-6) are found to be useful when the major frequency content in in question, while considerably higher orders have to be used for low-frequency component tracking. We show some examples and comparisons.

At the end we present an idea of quality evaluation of the linear model parameter estimation by using the autocorrelation of the inverse model output. Our research on the behavior of the autocorrelation function of random noise has shown that samples in the autocorrelation are normally distributed. Dependence of errors in parameter estimation and the behavior of autocorrelation has not yet been found explicitly, but we clearly demonstrated its presence.